今回はcart-pole問題をQ学習で解決します.
cart-pole問題とは以下の動画のように左右(1次元的)に動く滑車の上に回転軸まわりにのみ運動するように固定された振子を倒さないように滑車を制御(右か左に動かす)する問題です.
今回のポイントは状態をどのように把握するかです.
| Min | Max | |
|---|---|---|
| 滑車の位置 | -4.8 | +4.8 |
| 滑車の速度 | -∞ | +∞ |
| 棒の角度 | -0.418ラジアン(-24度) | +0.418ラジアン(+24度) |
| 棒の角速度 | -∞ | +∞ |
今回もQ学習で問題を解決していきます. 前回の三目並べと異なるのは,状態(state)が連続的に変化する点です. 滑車の位置を-4.8 -4.79999 -4.79998 … と細かく観測するようにすると,状態数が多すぎて学習が進まないうえに,利用可能な記憶容量を超えてしまいます. そのため,状態の観測の仕方を少し工夫する必要があります.
| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 滑車の位置 | -2.4未満 | -1.2未満 | 0未満 | 1.2未満 | 2.4未満 | 2.4以上 |
| 滑車の速度 | -3未満 | -1.5未満 | 0未満 | 1.5未満 | 3未満 | 3以上 |
| 棒の角度 | -0.28未満 | -0.14未満 | 0未満 | 0.14未満 | 0.28未満 | 0.28以上 |
| 棒の角速度 | -2.0未満 | -1.0未満 | 0未満 | 1.0未満 | 2.0未満 | 2.0以上 |
import numpy as np
import matplotlib.pyplot as plt
import gym
import random
Q_table = np.random.uniform(-1,1,(6**4,2))
# 評価値が最大になるように行動を選択する関数
def choice(state,Q_table,epsilon):
rnd = random.random()
if rnd < epsilon:
action = random.randint(0,1)
else:
state = return_index(state)
action = np.argmax(Q_table[state])
return action
# state をQ_table のインデックスに変換する関数
def return_index(state):
posit,Cvelo,angle,Pvelo = state
indQ1 = [np.digitize(posit, np.linspace(-2.4, 2.4, 5)),np.digitize(Cvelo, np.linspace(-3.0, 3.0, 5)),np.digitize(angle, np.linspace(-0.28, 0.28, 5)),np.digitize(Pvelo, np.linspace(-2.0, 2.0, 5))] #Qテーブルのどこを見るかがわかる
indQ2 = indQ1[0] + indQ1[1]*6 + indQ1[2]*(6**2) + indQ1[3]*(6**3) #それぞれが0~5まででこれを0~1295に1対1対応させたいので
return indQ2
# Q_tableを更新する関数
def Q_value(state,action,next_state,Q_table,reward,alpha,gamma):
state = return_index(state)
next_state = return_index(next_state)
Q_table[state,action] = Q_table[state,action] + alpha*(reward + gamma*max(Q_table[next_state]) - Q_table[state,action])
# 環境を'CartPole-v1'にする
env = gym.make('CartPole-v1')
score_list =np.zeros(1200)
for i in range(1200):
state = env.reset() # 最初の状態をstateに代入
epsilon = 0.7 - i/1000 # 徐々にεを下げていき,700以降ではランダムに動かなくする
for t in range(200):
# env.render() # 動きを動画で見たくないときにコメントアウトする
action = choice(state,Q_table,epsilon)
next_state, reward, done, info = env.step(action)
if done:
# 195stepより先に倒れてしまったら -200 の報酬
if t < 195:
reward = -200
else:
reward = 1
# 終わっていない間は1step耐えるごとに 1 の報酬
else:
reward = 1
Q_value(state,action,next_state,Q_table,reward,0.2,0.95)
state = next_state
if done: # done == True ならループを抜ける
break
print(f"{i}: {t+1} timestep後に倒れた")
score_list[i] = t
env.close() #環境を閉じる
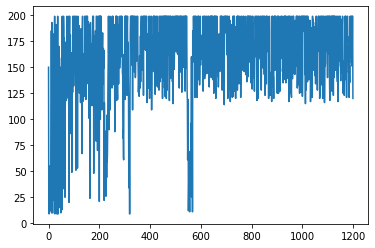
# グラフの描画
plt.plot(score_list)
plt.show()

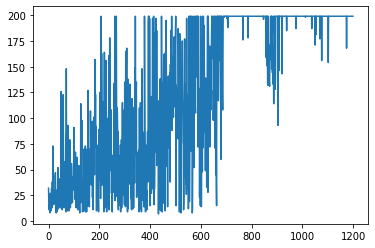

# ソフトマックス戦略で行動を選択する関数
def choice(state,Q_table):
rnd = random.random()
a = 0
state = return_index(state)
for i in range(2):
a += np.exp(Q_table[state][i])/(np.exp(Q_table[state][0])+np.exp(Q_table[state][1]))
if rnd < a:
action = i
break
return action
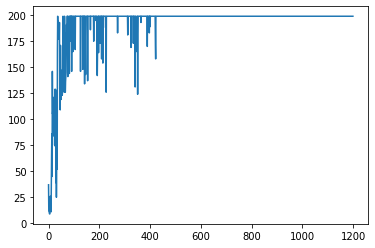
今回はソフトマックス戦略を用いてQ学習を行いました.