バンディットタスクでは予測価値の更新と探索を行うことにより報酬を最大化しようとしました. 今回は強化学習の手法で三目並べを解いてみたいと思います. まずは問題について整理します.
三目並べは先ほどの問題のように2つの予測報酬を比べるだけとはいきません. 問題を整理してみましょう. 三目並べの状態数: 三目並べは全9マスに〇 × 空白の3パターンのどれかが入る つまり,3^9通りの状態を持つ. 三目並べにおける行動: 全9マスのどこかに書き込むため9通りの行動が取れる. 三目並べにおける報酬: 勝った場合に報酬+1 負けた場合に報酬-1 三目並べにおける予測報酬: ある局面からその行動を取ったときにどの程度勝てそうか ある局面からその行動を取ったときにどの程度勝てそうか を経験に基づいて更新していくことで学習を進めます. ここで「ある局面からその行動を取ったとき」と簡単に言っていますが,状態数が3^9通り 行動がそれぞれの状態に対して9通り取れるため 9*(3^9)通りの予測報酬を記録しなければなりません.(実際は盤面の回転などを使えばこんなに考える必要はありませんが…) 大きな数字ですが,この程度なら普通のコンピュータで扱えます. 今回は「すべての局面に対して0~8の行動をそれぞれ取ったときに先手が勝つ確率」を予測価値にして問題を解いていきます.
前回学んだQ学習を三目並べに応用してみます. それほど難しくありません.やることは以下の4つです. 1. 局面とそれに対する行動の価値を保存するためのQ_table(評価値の表)を作る 2. Q_tableに従って行動する関数を作る 3. Q_tableを更新する関数を作る 4. たくさん対局させて学習させる 上から順に見ていきましょう. 1. 今回の場合は状態数が19683通り 行動が9通りなので大きさ19683×9の表を作ります. Q_table = np.random.uniform(-1,1,(19683,9))で一様乱数で初期化できます. 2. Q_tableに格納されるのは先手番の期待勝率なので,先手番ではこれが最大になるように 後手番ではこれが最小になるように行動を選びます. これは np.argmax(Q_table[state]) と書けます. 3. Q_tableを更新する関数を作ります.ここで気を付けなければいけないのは次の状態を考慮する gamma*(max(V[next_state]) の部分です. state next_state の順番でゲームが進むとします. 自分が先手の場合はQ_table[state]が最大となる[action]を選びます. 後手は先手の勝率が最小となるように行動するためQ_table[next_state]が最小となるような[action]を選びます. next_stateが終わった状態での評価値はgamma*(max(V[next_state])ではなくgamma*(min(V[next_state])にする必要があります. 一人でプレイするゲームの場合は,gamma*(max(V[next_state])でよいのですが,今回のような行動選択のルール(最小を取るか 最大を取るか)が変わるゲームでは注意が必要になります. 4. ループを使ってたくさん対局させて学習させます. 実際のコードが以下の通りです. 綺麗なコードではないのでわかる方は適宜修正して使ってみてください.
import numpy as np
import matplotlib.pyplot as plt
class tictactoe:
def __init__(self):
self.board = np.zeros(9,dtype=int)
# 状態の番号を返す関数
def state(self):
state = 0
for i in range(9):
state += self.board[i]*(3**i)
return state
# 勝敗を判定し勝負がついていなければ0 先手が勝ちなら1 後手が勝ちなら2 引き分けなら3を返す関数
def judge(self):
# 横の判定
for i in range(3):
if self.board[3*i] == self.board[3*i+1] == self.board[3*i+2]:
return self.board[3*i]
# 縦の判定
for i in range(3):
if self.board[i] == self.board[3+i] == self.board[6+i]:
return self.board[i]
# 斜めの判定
if self.board[0] == self.board[4] == self.board[8]:
return self.board[0]
if self.board[2] == self.board[4] == self.board[6]:
return self.board[2]
if not 0 in game.board:
return 3
else:
return 0
# 指定された場所を埋める関数
def put(self,ind,color):
if self.board[ind] == 0:
self.board[ind] = color
return 0
else:
return 1
# Q学習エージェント turnは先手なら1 後手なら2
def getchoiceQ(Q_table,game,epsilon,turn=1):
rnd = np.random.rand()
if not 0 in game.board:
return 0
# 一定の確率εでランダムに行動する
if rnd < epsilon:
put_ind = np.random.randint(0,9)
while game.put(put_ind,turn):
put_ind = np.random.randint(0,9)
return put_ind
else:
# 自分が先手番なら評価値を最大にするように行動
if turn == 1:
put_ind = np.argmax(Q_table[game.state()])
while game.put(put_ind,1):
Q_table[game.state(),put_ind] -= 100 # 置けないところに置いたら違法な行動の評価値を-100してやり直す
put_ind = np.argmax(Q_table[game.state()])
# 自分が後手番なら評価値を最小にするように行動する
else:
put_ind = np.argmin(Q_table[game.state()])
while game.put(put_ind,2):
Q_table[game.state(),put_ind] += 100 # 置けないところに置いたら違法な行動の評価値を+100してやり直す
put_ind = np.argmin(Q_table[game.state()])
return put_ind
# ランダムに行動するエージェント
def random_choice(game):
put_ind = np.random.randint(0,9)
while game.put(put_ind,2):
put_ind = np.random.randint(0,9)
return 0
# 人間がプレイする場合に使う関数
def human_choice(game):
put_ind = int(input())
while game.put(put_ind,2):
put_ind = int(input())
return 0
# Q_tableを更新する関数
def Q_update(Q_table,current,put_ind,next_state,reward,alpha,gamma,turn):
if turn == 1:
Q_table[current,put_ind] = Q_table[current,put_ind] + alpha*(reward + gamma*min(Q_table[next_state]) - Q_table[current,put_ind])
if turn == 2:
Q_table[current,put_ind] = Q_table[current,put_ind] + alpha*(reward + gamma*max(Q_table[next_state]) - Q_table[current,put_ind])
# 一様乱数で初期化
Q_table = np.random.uniform(-1,1,(3**9,9))
alpha = 0.1 # 学習率
gamma = 0.99 # 割引率
epsilon = 1.1 # ランダムに行動する確率
ite = 10000 # 繰り返し回数を指定
for k in range(10):
game = tictactoe()
epsilon -= 0.1
Win = np.zeros(ite,dtype=int)
Draw = np.zeros(ite,dtype=int)
for i in range(ite):
game = tictactoe()
while True:
current = game.state()
put_ind = getchoiceQ(Q_table,game,epsilon)
next_state = game.state()
if game.judge() == 1:
Q_update(Q_table,current,put_ind,next_state,100,alpha,gamma,1)
Q_update(Q_table,current2,put_ind2,next_state2,100,alpha,gamma,2)
Win[i] += 1
break
if game.judge() == 3:
Q_update(Q_table,current,put_ind,next_state,0,alpha,gamma,1)
Q_update(Q_table,current2,put_ind2,next_state2,0,alpha,gamma,2)
Draw[i] += 1
break
if game.judge() == 0:
try:
Q_update(Q_table,current2,put_ind2,next_state2,0,alpha,gamma,2)
except:
pass
current2 = game.state()
put_ind2 = getchoiceQ(Q_table,game,epsilon,2)
next_state2 = game.state()
if game.judge() == 2:
Q_update(Q_table,current,put_ind,next_state,-100,alpha,gamma,1)
Q_update(Q_table,current2,put_ind2,next_state2,-100,alpha,gamma,2)
break
if game.judge() == 3:
Q_update(Q_table,current,put_ind,next_state,0,alpha,gamma,1)
Q_update(Q_table,current2,put_ind2,next_state2,0,alpha,gamma,2)
Draw[i] += 1
break
if game.judge() == 0:
Q_update(Q_table,current,put_ind,next_state,0,alpha,gamma,1)
# ---------------------------------------------------------
print(f"epsilon = {epsilon:.1f}")
print(f"勝率:{sum(Win)/(ite):.2%}")
print(f"引き分け:{sum(Draw)/(ite):.2%}")
print(f"負け:{1-(sum(Win)/(ite))-(sum(Draw)/(ite)):.2%}")
print()
print("学習終了!")
alpha=0.1 gamma=0.99 epsilonは対局数が少ないうちはランダムに行動する確率が高くなるように0.1<=epsilon<=1 の範囲で設定しました(初期のうちは探索を多く行いたいため) rewardは先手が勝ったときに+100 後手が勝った時に-100を与えています. 対局を繰り返す部分ではデータの偏りを減らすために自己対局ではなくランダムと対局させた方が学習が安定するかもしれませんが, 手元で試した限り問題なさそうだったので自己対局としています.
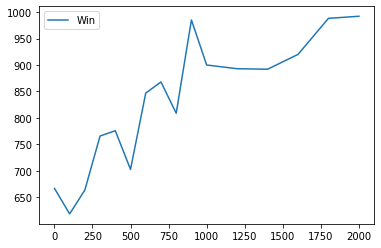
上のコードを動かす前にどのように学習が進むのかを実験してみましょう. 以下はalpha=0.1 gamma=0.99 reward=±100 学習回数が[1,100,200,300,400,500,600,700, 800,900,1000,1200,1400,1600,1800,2000]のときに 先手Q学習 後手ランダムで1000回戦った場合の勝ち数と負け数のグラフです.

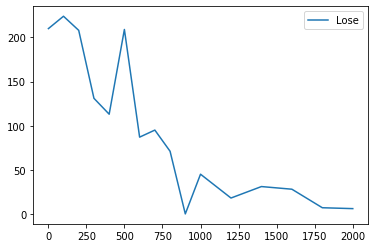
その他の変数に学習率 割引率 報酬 があります. 学習率は大きければ学習が速くなりますが,安定しなくなります. 割引率に関しても大きすぎると序盤の学習が遅くなるかもしれません(?) 報酬に関しては学習回数と同じように試してみましたが,Q_tableの初期値に対して小さすぎる報酬でなければしっかり学習が進みました. (報酬0.1で2000回学習してもほとんど進みませんでした.)
それでは上のコードを使って学習させてみましょう. 学習回数が大きいほど強くなることが分かっています. とりあえず対局を繰り返すコードのiteを3000に変えて学習させます. 学習が終了すると「学習終了」と表示されます.1分もあれば終わると思います. 学習が終了したら以下のコードでランダムと1000回対戦し勝率を確認することができます.
game = tictactoe()
ite = 1000
R = np.zeros(1000,dtype=int)
Draw = np.zeros(1000,dtype=int)
# epsilon=1 はランダムと同じ
epsilon_1p = 0 # 先手のepsilon
epsilon_2p = 1 # 後手のepsilon
for i in range(ite):
game = tictactoe()
while True:
put_ind = getchoiceQ(Q_table,game,epsilon=epsilon_1p)
if game.judge() == 1:
R[j] += 1
break
if game.judge() == 3:
Draw[j] += 1
break
put_ind2 = getchoiceQ(Q_table,game,epsilon=epsilon_2p,turn=2)
if game.judge() == 2:
break
if game.judge() == 3:
Draw[j] += 1
break
# ---------------------------------------------------------
print(f"勝率:{sum(R)/(ite):.2%}")
print(f"引き分け:{sum(Draw)/(ite):.2%}")
print(f"負け:{1-(sum(R)/(ite))-(sum(Draw)/(ite)):.2%}")
以下のコードでAIと対戦することができます.
0,1,2
3,4,5
6,7,8
という番号で対応する場所を埋められます.
# 人間と対局
# どちらかのepsilonを0にすることでランダム対局
game = tictactoe()
while True:
put_ind = getchoiceQ(Q_table,game,epsilon=0)
# human_choice(game,turn=1)
for i in range(3):
print(game.board[3*i],game.board[3*i+1],game.board[3*i+2])
print()
if game.judge() != 0:
break
# put_ind2 = getchoiceQ(Q_table,game,epsilon=0,turn=2)
human_choice(game,turn=2)
for i in range(3):
print(game.board[3*i],game.board[3*i+1],game.board[3*i+2])
print()
if game.judge() != 0:
break
# ---------------------------------------------------------
if game.judge() == 3:
print("引き分け")
elif game.judge() == 2:
print("後手の勝ち")
else:
print("先手の勝ち")
ご存じの方もいらっしゃるかもしれませんが,このゲーム 最善手を取り続けると必ず引き分けになります. 30000回の学習でも結構強いです.負けなしのAIができた方もいるかもしれません.
今回はQ学習によって三目並べAIを作りました. 次回はQ学習によってカートポール問題を解いてみたいと思います.