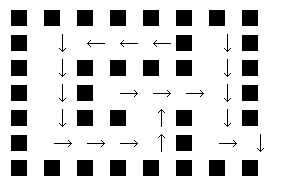
三目並べを解く前に迷路の例を使ってQ学習という強化学習の手法についてご紹介します. 次のような4×6の迷路を考えます.

先ほどのバンディットタスクでは報酬が行動に従ってのみ決まったため,A,Bを引く行動がどの程度の報酬をもたらすか
つまり行動の持つ価値を更新することにより学習を進めました.
今回の迷路では 自分の位置 と その場所で取る行動 の組み合わせで考える必要があります.
つまり,状態(state)と行動(action)をセットで考える必要があります.
そこでV[state][action]を「stateでactionを取った場合の予測報酬」とします.
さらに前回はそれぞれの行動が次の報酬に影響を与えない 独立したものであったのに対し,今回はそれぞれの行動により状態が遷移していきます.
例えば,state=[0,0]で右に進んだらstate=[1,0]に遷移します.
今回は移動後の状態がどの程度良いものであるかを評価する必要もあるのです.
従って,以下のような式で予測報酬を更新します.
state:状態 next_state:遷移後の状態 action:行動 reward:報酬 alpha:学習率 gamma:割引率
V[state][action] += alpha*(reward + gamma*(max(V[next_state]) - V[state][action])) (※1)
gamma*(max(V[next_state]) の部分を取り除いてしまえばやっていることは前回と同じです.
(max(V[next_state]) は次の局面で最適な行動を取った場合の予測報酬を示しています.
S1,S2,S3, … のようにゲームが進んでいくとすると,S1ではS2の価値も考慮し,S2はS3の価値を考慮する,S3は…
と言ったように先読みをすることができるようになります.
しかし,先の展開を読もうとすれば読もうとするほど難しくなります.より詳しくは予測価値の精度が落ちます.
3手詰めの詰将棋より7手詰めの詰将棋の方が難しいようなものです.
そこで未来に得られそうな報酬をどの程度参考にするかを 0 < gannma <= 1で決めます.
これを割引率と言います.
割引率が高ければ高いほど即時報酬を重視するようになります.
このように,状態と行動の組み合わせの報酬を更新することで行動を学習する方法をQ学習と言います.
(※1) この式は V[state][action] = V[state][action] + alpha*(reward + gamma*(max(V[next_state]) - V[state][action])) と書かれることも
多いですが,見た目が少し違うだけで全く同じものです.
maze = np.zeros((7,8),dtype=int)
maze[0] = 1
maze[6] = 1
for i in range(7):
maze[i][0] = 1
maze[i][7] = 1
maze[2][2:6] = 1
maze[1][5] = 1
maze[4][2:4] = 1
maze[4][5] = 1
maze[5][5] = 1
maze[3][2] = 1
maze[5][7] = 0
print(maze)
import random
# 上:0 下:1 左:2 右:3
# 行動を選択する関数
def Q_agent(Q_table,pos,epsilon):
rnd = random.random()
state = pos_to_state(pos)
if epsilon < rnd:
action = random.choice([0,1,2,3])
else:
action = np.argmax(Q_table[state])
return action
# 価値の更新を行う関数
def Q_update(Q_table,state,action,reward,next_state,alpha,gamma):
Q_table[state][action] += alpha*(reward + gamma*max(Q_table[next_state]) - Q_table[state][action])
# 位置を移動する関数
def move(pos,action):
if action == 0:
if maze[pos[0]-1][pos[1]] == 0:
pos[0] -= 1
elif action == 1:
if maze[pos[0]+1][pos[1]] == 0:
pos[0] += 1
elif action == 2:
if maze[pos[0]][pos[1]-1] == 0:
pos[1] -= 1
else:
if maze[pos[0]][pos[1]+1] == 0:
pos[1] += 1
# 位置と状態番号を対応させる関数
def pos_to_state(pos):
state = (pos[0]-1)*7 + (pos[1]-1)
return state
# ゴールしているかを判定する関数
def goal_or_not(pos):
if pos == [5,7]:
return True
else:
return False
Q_table = np.random.uniform(-1,1,(35,4))
# 100回の移動を1セットとしゲームを300回繰り返す
for j in range(300):
pos = [1,1]
for i in range(100): # 100回1セットで迷路をプレイ
state = pos_to_state(pos)
action = Q_agent(Q_table,pos,epsilon=0.5)
move(pos,action)
next_state = pos_to_state(pos)
if goal_or_not(pos):
Q_update(Q_table,state,action,10,next_state,alpha=0.2,gamma=0.9)
break # ゴールしたら終了
else:
Q_update(Q_table,state,action,-1,next_state,alpha=0.2,gamma=0.9)
for i in range(7):
for j in range(8):
if maze[i][j] == 1:
print("■",end=" ")
else:
state = pos_to_state([i,j])
if np.argmax(Q_table[state]) == 0:
print(" ↑",end="")
elif np.argmax(Q_table[state]) == 1:
print(" ↓",end="")
elif np.argmax(Q_table[state]) == 2:
print(" ←",end="")
elif np.argmax(Q_table[state]) == 3:
print(" →",end="")
print()