今回は素因数分解をしていきたいと思います.
素朴な問題ですが,暗号技術に関連してくるテーマです.
ところで最初に順番に読み進めなくても大丈夫と言ったのですが,第2回のみ第1回の内容と強く関連しています.
第1回の素数判定のページを読んでからこのページに戻っていただけると理解が深まります.
与えられた入力nに対して素因数分解を返すプログラムを書きたい
すべての素因数を求めたいのですから2からn-1までの数で割ってしまえば,簡単に素因数分解ができそうですね. さらに素数判定のときの要領で2からint(√n)までの数に限定すれば無駄を省けます.
n = int(input())
n_ = n # 元々のnを記憶しておく
div_list = [] # 素因数のリストを作る
num = 2 # 2から割り始める
while num <= int(n_**0.5)+1: # 割る数がint(n_**0.5)+1以下の間 繰り返す
if n%num == 0:
div_list.append(num) # 割り切れたら素因数のリストに追加
n = n/num # nを更新する
else:
num += 1 # 割り切れなければ次の数を試す
if n < num:
break # 割る数のほうがnより大きくなったら終了
# n が1でなければそれも素因数なので追加
if n != 1:
div_list.append(int(n))
print(div_list)
1からnまでの素因数分解を全て求めたい.
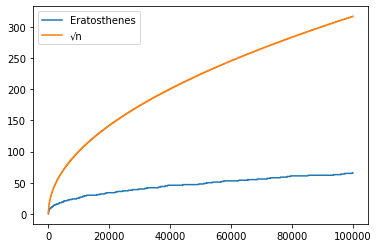
計算量O(√n)の素因数分解をn回行うのでO(n√n)の計算量です.(section1 の実行時間と大きくかけ離れる理由は実験中)
n = int(input())
div_list = [[] for i in range(n+1)] # 素因数のリストを作る
for num in range(n+1):
n_ = num # 元々のnを記憶しておく
div_num = 2 # 2から割り始める
while div_num <= int(n_**0.5)+1: # 割る数がint(n_**0.5)+1以下の間 繰り返す
if num%div_num == 0:
div_list[n_].append(div_num) # 割り切れたら素因数のリストに追加
num = num/div_num # nを更新する
else:
div_num += 1 # 割り切れなければ次の数を試す
if num < div_num:
break # 割る数のほうがnより大きくなったら終了
# n が1でなければそれも素因数なので追加
if num != 1:
div_list[n_].append(int(num))
for i in range(2,len(div_list)):
print(i,end="=")
for j in range(len(div_list[i])):
if j == len(div_list[i]) - 1:
print(div_list[i][j])
else:
print(div_list[i][j],end="*")
n = int(input())
num_list = [True for i in range(n+1)]
num_list[0] = False
num_list[1] = False
# エラトステネスの篩
for i in range(2,int(n**0.5)+1):
if num_list[i] == True:
p = i
for j in range(p*p,n+1,p):
num_list[j] = False
prime_list = []
for i in range(n+1):
if num_list[i]:
prime_list.append(i)
# ここから素因数分解
div_list = [[] for i in range(n+1)] # 素因数のリストを作る
for num in range(n+1):
ind = 0
n_ = num # 元々のnを記憶しておく
div_num = 2 # 2から割り始める
while div_num <= int(n_**0.5)+1: # 割る数がint(n_**0.5)+1以下の間 繰り返す
div_num = prime_list[ind] # 2から割り始める
if num%div_num == 0:
div_list[n_].append(div_num) # 割り切れたら素因数のリストに追加
num = num/div_num # nを更新する
else:
ind += 1 # 割り切れなければ次の数を試す
if num < div_num:
break # 割る数のほうがnより大きくなったら終了
# n が1でなければそれも素因数なので追加
if num != 1:
div_list[n_].append(int(num))

n = int(input())
min_factor = [False for i in range(n+1)]
min_factor[0] = True
min_factor[1] = True
# 最小の素因数を求める
for i in range(2,int(n**0.5)+1):
if min_factor[i] == False:
p = i
min_factor[i] = p
for j in range(p*p,n+1,p):
if min_factor[j] == False:
min_factor[j] = p
for i in range(n+1):
if min_factor[i] == False:
min_factor[i] = i
# 最小の素因数を使って素因数分解を行う
div_list = [[] for i in range(n+1)]
for num in range(2,n+1):
num_ = num
while num > 1:
div_list[num_].append(min_factor[num])
num = int(num/min_factor[num])
今回は素因数分解をして遊んでみました. 興味がある方は,素因数分解と暗号技術の関連についても調べてみると面白いですよ. 余裕があればこれについても書いてみたいと思います. 最小公倍数・最大公約数について考えてみたいと思います.