
バンディットタスクについてです. バンディットタスクとは何かについて説明した後に問題を解くいくつかの戦略とその特徴について簡単に解説します. ページの最後に今回使ったコードを載せておきます. このページは『これからの強化学習』の多腕バンディット問題の節(6Pから13P)を参考にしています.
何個かのスロットマシーンがあるとします. それぞれにスロットを回すと確率に応じて報酬1を得ることができますが,それぞれのスロットの当たり確率は分かりません. このような状況で得られる報酬を最大化する戦略を考えます. 以下ではスロットマシーンが4つで引ける回数が10000回の場合で考えます. それぞれのスロットマシーンの当たり確率は0.2,0.3,0.4,0.5とします. 戦略の性能評価は10000回を1セットとして1000セットをプレイさせ,最適なスロットを選んだ回数と得られた報酬の平均で行います.
人間であればそれぞれのスロットマシーンを何回かずつ試してみて得られる報酬の期待値が大きそうなものを選ぶと思います.
例えば最初に100回ずつ試し打ちしてみて得られた報酬が一番大きかったスロットマシーンを回すような戦略です.
このような戦略で何回か試してみると4000から5000程度の報酬が得られました.
また,1000回試すと平均して4840程度の報酬が得られました.最適なスロットを選んだ割合は88%程度でした.
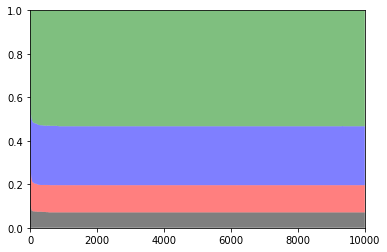
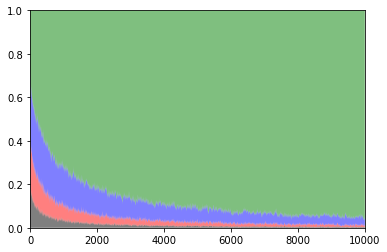
以下は各スロットを選択した確率のグラフです.
緑:払い戻し率0.5 青:払い戻し率0.4 赤:払い戻し率0.3 黒:払い戻し率0.2


得られる報酬をなるべく大きくするにはどうすればいいでしょうか? それは「探索」と「活用」のバランスを上手くとることです. 「探索」は上の実験で言えば「最初に100回引いてみる」の部分です. スロットマシーンの実際の価値を試してみて評価するような動きです. 「活用」は上の実験で言うところの試し終わった後にそのスロットマシーンを引き続ける部分です. 探索で得られた予測価値を活用して得られる報酬を最大化しようとしています. 探索の回数が少なすぎれば,実際の価値とはかけ離れた見積もりをしてしまい得られる報酬が少なくなってしまいます. 逆に探索の回数が多すぎても,実際には価値の低いスロットマシーンを何度も試すことになるので得られる報酬は少なくなります. また上の実験では簡単のため「探索」と「活用」を明確に分ける戦略を用いましたが,通常は「活用」で得られたデータによっても予測価値を更新します. 以下では,「探索」と「活用」のバランスを取るいくつかの戦略とその特徴をまとめます.
予想価値をこれまでに得た報酬の平均 つまり 標本平均とし,予想価値が最大になるものを選ぶ戦略を考えます.
ただし,一度も引いていないものがある場合はそのスロットを試します.
価値が最大になるものを選ぶ戦略を貪欲法やグリーディ戦略と呼びます.
予想価値の初期値は0とします.
1000回プレイしたときの平均報酬は4260程度です.最適なスロットを選んだ割合は53%程度でした.
以下は各スロットを選択した確率のグラフです.
緑:払い戻し率0.5 青:払い戻し率0.4 赤:払い戻し率0.3 黒:払い戻し率0.2
低すぎる初期値を用いた場合に問題が起きてしまうことが分かったので今回は初期値を「高め」に設定してみます.
今回は1回スロットを回して得られる報酬の最大値が1であることが分かっているため,予想価値の初期値を1とします.
このような高い初期値を「楽観的初期値」と言います.
また,予想価値valueの更新をvalue += alpha×(reward-value) (alpha:定数)で行います.
これは,予想と実際の報酬の誤差に学習率alphaをかけたものを足しています.
誤差が大きいほど大きく更新され,予想と実際の報酬が一致していれば更新は行われません.
1000回プレイしたときの平均報酬は4850程度です.最適なスロットを選んだ割合は87%程度でした.
以下は各スロットを選択した確率のグラフです.
緑:払い戻し率0.5 青:払い戻し率0.4 赤:払い戻し率0.3 黒:払い戻し率0.2
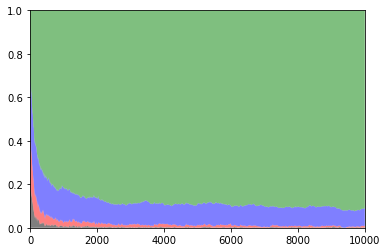
「高め」の初期値を採用したところ上手く探索を行うようになりましたが,そもそも「高め」が分からない問題を解きたい場合もあります.
例えば,スロットマシーンの報酬が期待値が未知の正規分布に従う場合などは「高め」が分かりません.
そこで初期値はテキトーに決め,ある一定の割合εで探索を行うようにすることを考えます.
ε=0.1として実験してみます.予想報酬の初期値はテキトーに0にしておきます.
1000回プレイしたときの平均報酬は4810程度です.最適なスロットを選んだ割合は89%程度でした.
以下は各スロットを選択した確率のグラフです.
緑:払い戻し率0.5 青:払い戻し率0.4 赤:払い戻し率0.3 黒:払い戻し率0.2
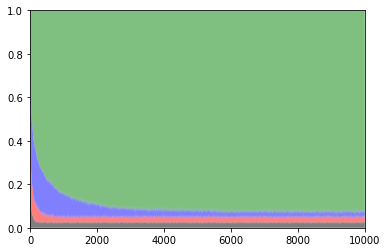
ε-グリーディ戦略をもう少し改良します.
ε=0.1と固定の数値を使っていましたが,最初の方はそれぞれの予想価値が正確でない可能性が高いのでより積極的に探索を行いたいです.
逆に回数を重ねてくるとある程度正確な予想価値が求まっているため探索をすると無駄が発生するので探索の頻度を減らしたいです.
そこで引いた回数が増えるにつれてεを減衰させていくことを考えます.
最初の3000回でε=1からε=0.1まで減衰させます.
1000回プレイしたときの平均報酬は4650程度です.最適なスロットを選んだ割合は82%程度でした.
以下は各スロットを選択した確率のグラフです.
緑:払い戻し率0.5 青:払い戻し率0.4 赤:払い戻し率0.3 黒:払い戻し率0.2.
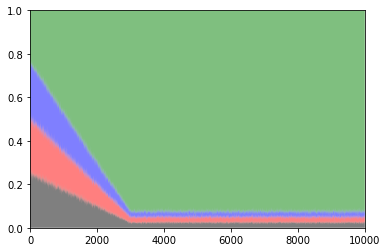
ソフトマックス関数という関数を用いて予想価値にもとづいて行動を選択します.
ソフトマックス関数はそれぞれの行動を選ぶ確率を返します.



これまでの標本平均に基づく予想価値ではなく以下の式で期待報酬の予想を行います.

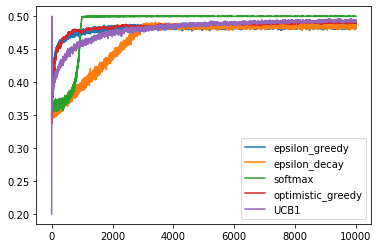
全ての戦略の報酬の推移のグラフです. 序盤に特に差が見られます.
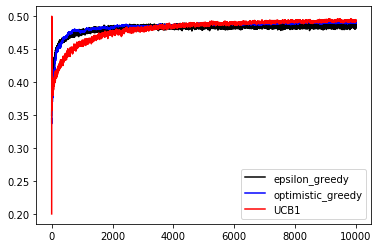
バンディットタスクに関していくつかの戦略を試してみました. 性能評価に関してはあくまで10000回 0.2,0.3,0.4,0.5の確率という設定の下の評価であるため,問題設定が変われば性能評価も変わってきます. それぞれ特徴があるため,問題の設定に合わせてどの戦略を用いるべきなのかを考えることが重要です.